Post

NeRF:Representing Scenes as Neural Radiance Fields for View Synthesis

<논문리뷰> NeRF에 대하여

Posted
By Chaewon Mun
18 min read

https://arxiv.org/pdf/1706.03762v7

Abstract & Method

  • 3D Object 자체를 렌더링하는 것이 아닌 Novel View Synthesis한 분야에서 3D Object를 바라본 모습을 예측할 수 있는 모델을 만들 수 있게 한다.
  • ray에 따라 입력의 5D 좌표를 querying하고, volume rendering 기술을 사용해 출력된 색상과 밀도를 이미지로 투영함으로써 시점을 합성한다.
  • 물체 하나에 대해 모든 위치에 대해 원하는 값이 나오도록 각 scen3마다 학습하는 rendering 과정이여서 현재 데이터에 일종의 overfitting하는 영역이라 볼 수 있다.

Introduction

NeRF는 연속적인 5D scene 표현의 파라미터를 MLP로 최적화하여 view synthesis 문제를 해결하기 위해 다음과 같은 단계를 수행한다.

  • [Overall Process]
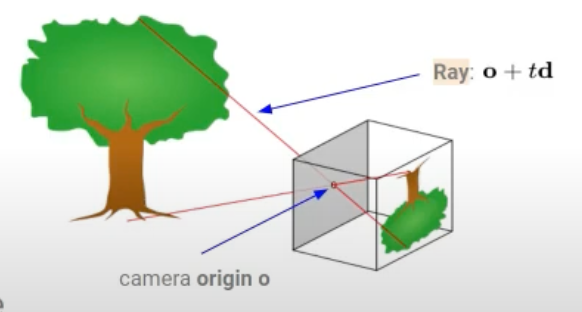
    1. 2D Pixel 좌표마다 View Direction(θ,ϕ) 방향으로 scene을 통해 ray를 이동시킨다.
    2. ray 위에 N개의 3D Voxel 좌표(x,y,z)를 Sampling해 3D point sets을 생성한다.
    3. N개 중 i번째 3D Voxel 좌표와 View Direction(θ,ϕ)를 MLP의 입력 값으로 넣어 volume density($σ_i$) 와 radiance($c_i$  = RGB)를 예측한다. 다시말해, volume rendering 기술을 사용해 색상과 밀도를 2D 이미지로 누적한다.
    4. pixel마다 실제 관찰된 이미지의 색상값과 rendering된 대응시점의 예측한 값으로 loss 값을 계산한다.
    5. back-propagation으로 이 오류를 최소화해 실제 위치에 높은 volume density와 정확한 color를 할당해 일관된 장면 표현을 최적화한다.

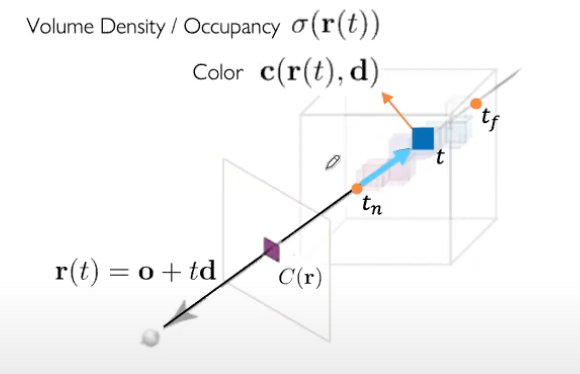
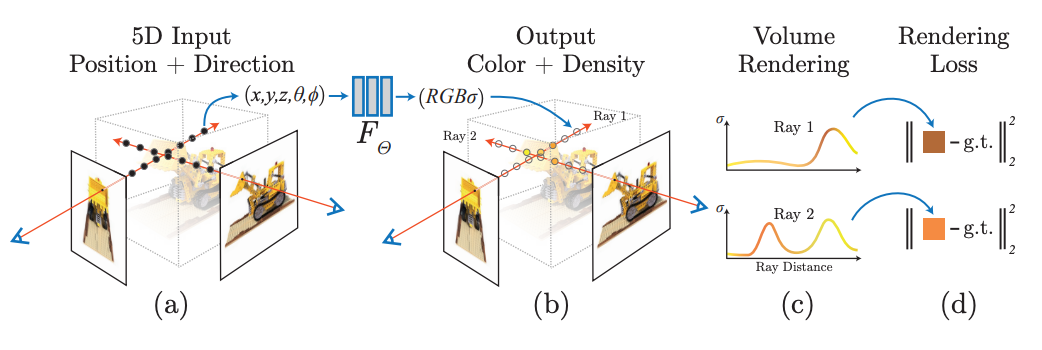    An overview of our nerf scene representation and differentiable rendering procedure

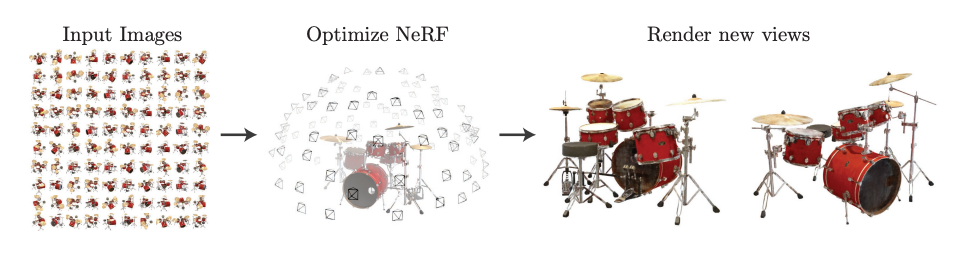input image sets으로부터 scene의 연속적인 5D NeRF representation를 최적화

Neural Radiance Field(NeRF) Scene Representation

: scene을 NeRF로 모델링하고 새로운 시점을 렌더링하기 위해 가중치 Θ를 최적화하는 과정을 설명한다

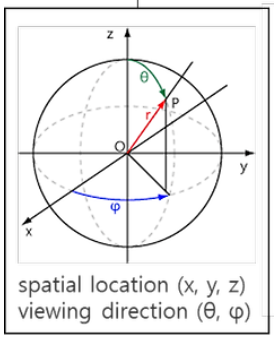
  • Input: 단일 연속 5D(x,d) 좌표
    • 3D 공간위치: x = (x, y, z)
    • 2D 시점방향: d = (θ, φ)
  • Output: c, σ
    • 방출된 색상: c = (r, g, b)
    • volume density == 투명도의 역수: σ

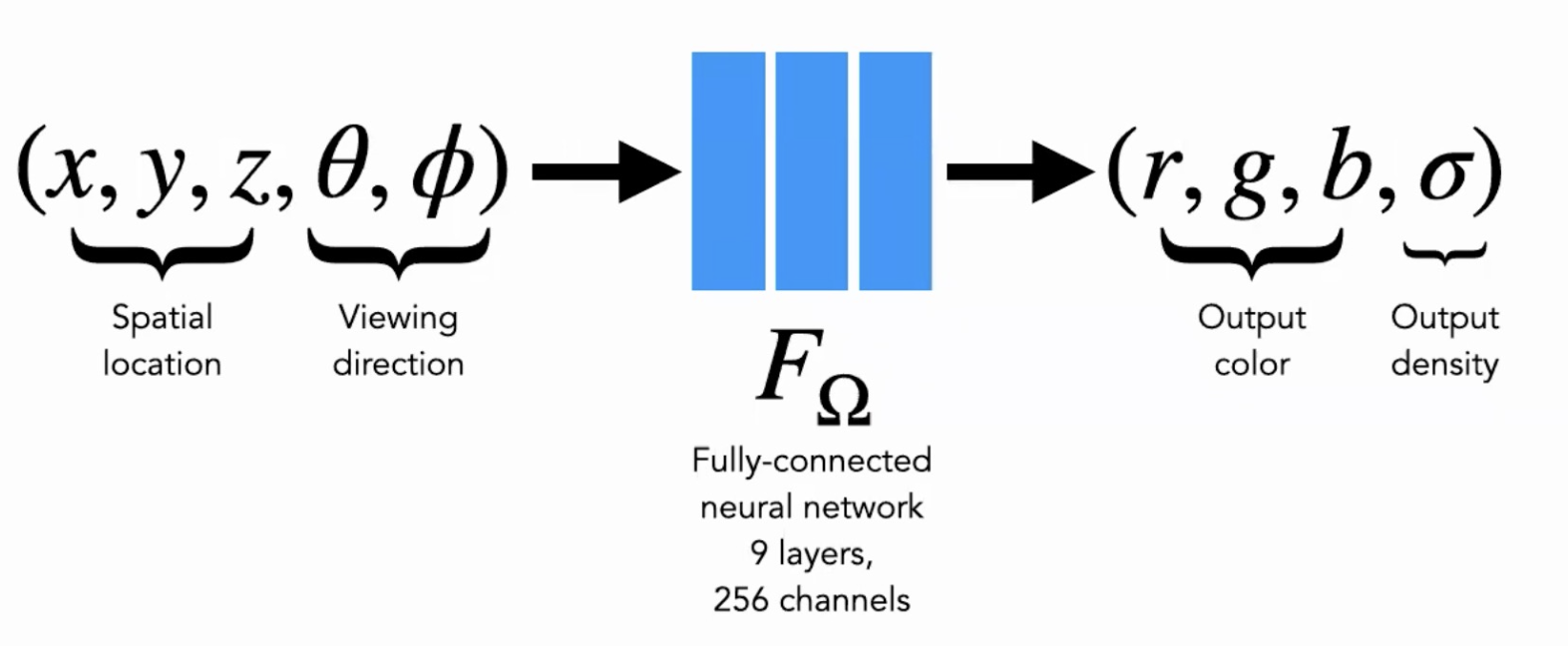
  • 네트워크는 위치 x만으로 volume density σ를 예측하고, RGB 색상 c는 direction 정보가 들어간 5D input으로 예측한다.

    이를 위해, MLP FΘ는 먼저 입력된 3차원 좌표 x를 9개의 fully-connected layers(256 channels)로 처리하고, σ와 256차원의 특징 벡터를 출력합니다.

    이 특징 벡터를 ray의 viewing direction과 연결하여, view-dependent한 RGB 색상을 출력하는 추가 fully-connected layer로 전달한다.

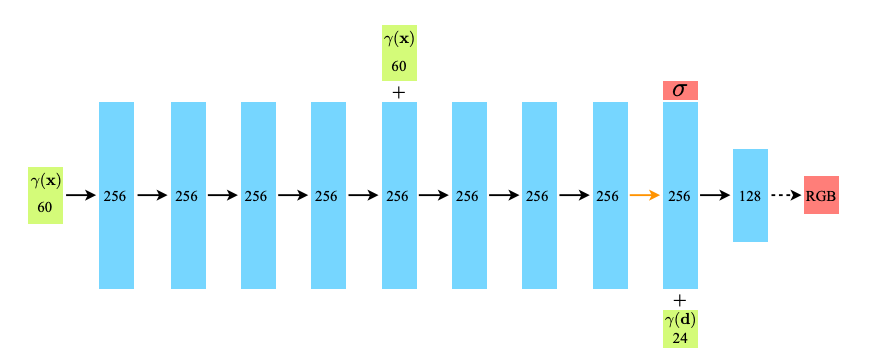[MLP Architecture] 위에 구조에 따르면 입력 layer에서 위치정보 x(x,y,z) 전달 → 5th layer에서 skip-connection으로 위치정보 전달 → 9th layer에서 density 출력, 방향정보 d가 입력되어 최종적으로 RGB가 출력된다.

Volume Rendering with Radiance Fields

  • NeRF의 Training 과정

    : shoot ray → render ray to pixel → minimize reconstruction error via backpropagation

    • supervised learning을 사용하기 때문에 학습에 정답데이터(Ground Truth_GT)가 필요하다.
    • 이미지 입력(카메라 시점(𝜃,𝜙)와 voxel 좌표(x,y,z))은 이미 가지고 있는 뷰를 예측하도록 모델을 학습시키고, 실제 view를 예측하도록 예측값과 실제값 사이의 loss을 계산하여 학습한다.

→ 연속적인 NeRF에서 시점을 렌더링하기 위해서는 원하는 가상 카메라의 각 pixel을 통과하는 ray에 대해 적분 C(r)을 추정해야 한다.

  • Projection
    • Density가 클수록 weight가 커야한다. → $\sigma(r(t))$
    • 그 지점을 가로막고 있는 점들의 Density 합이 작을수록 weight가 커야한다. → T(t)

    ⇒ 모든점의 RGB, Density 값을 추정해 얼마나 가중치가 부여됐느냐에 따라 적절한 최종 컬러값을 계산한다.

  • Objective Function
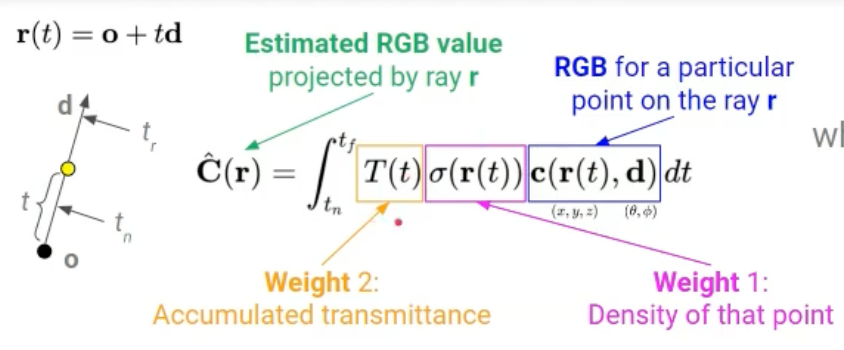
    • C(r): 근거리와 원거리 경계 $t_n$과 $t_f$ 사이에서의 ray r로부터 추정된 RGB 값
    • r(t) = o + td → Ray

    • $c(r(t), d)$: RGB

    • Weight 1: $\sigma(r(t))$ : density of that point

      아무것도 없는 경우 random한 color 값을 반환하는 것을 방지하기 위해

      • 물체가 없을 때: 0 → RGB값이 더해지지 않음
      • 물체가 있을 때: 1 → RGB값이 더해짐

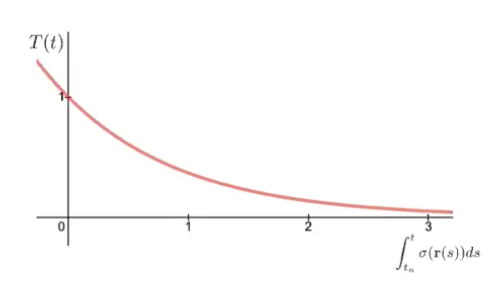
    • Weight 2: T(t): Accumulated transmittance

      광선이 $t_n$에서 t까지 다른 입자에 부딪히지 않고 이동할 확률을 나타내는 누적 투과도

      • $t_n$: 물체가 시작되는 점 ~ $t$: 현재 점
      • 누적된 밀도의 적분값을 지수함수로 변환한 값으로 밀도가 커지면 $\sigma(r(s))$값이 커지고 이에 따라 T(t)가 급격하게 감소해 0에 가까워진다. → 해당 구간에서 광선이 다른 물체에 의해 많이 차단되었음을 의미한다.

\[C(r) = \int_{t_n}^{t_f} T(t) \sigma(r(t)) c(r(t), d) \, dt,\quad T(t) = \exp\left(- \int_{t_n}^{t} \sigma(r(s)) \, ds \right)\]

최종적으로 C(r)은 $t_n$에서 $t_f$까지의 점들의 ‘투과도 x density x color(rgb)’를 적분해 volume rendering을 완성하게 된다.

Optimizing a Neural Radiance Field

  • 최적화 방법 ⇒ Positional Encoding & Hierarchical Sampling
    1. Positional encoding of the input coordinates → MLP가 고주파 함수를 표현하는 데 도움을 준다.
    2. hierarchical sampling procedure → 고주파 표현을 효율적으로 샘플링할 수 있도록 한다.

Positional encoding

네트워크 $F_\Theta$ 가 $\text{xyz}\theta\phi$ 입력 좌표를 직접 처리하면 3D 위치 정보와 2D 방향 정보는 원래 저차원이기 때문에 색상과 고주파 변화를 제대로 표현하지 못하는 렌더링 결과가 나타나는 것을 발견했다.

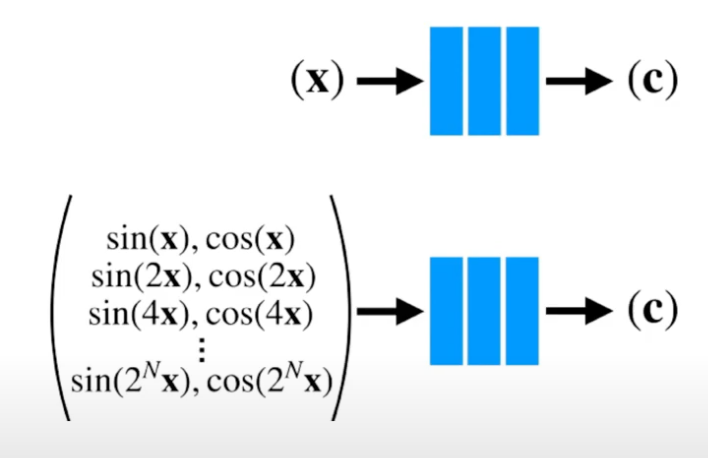
따라서, 입력을 네트워크에 전달하기 전에 고주파 함수를 사용한 Positional Encoding을 통해 입력 데이터를 고차원으로 임베딩하여 MLP가 더 다양한 정보를 활용할 수 있도록 $F_\Theta$를 두 개의 함수 $F_\Theta = F{\prime}_\Theta \circ \gamma$ 의 합성으로 재구성해 MLP가 고주파 함수를 더 쉽게 근사할 수 있도록 한다.

$\gamma$: $\mathbb{R}^3$에서 더 높은 차원의 공간 $\mathbb{R}^{2L}$ 으로의 매핑

  • 좌표를 고차원 공간으로 올려 구분성을 잘 주기 위해 sin, cos 사용
\[\gamma(p) = \left( \sin(2^0\pi p), \cos(2^0\pi p), \ldots, \sin(2^{L-1}\pi p), \cos(2^{L-1}\pi p) \right).\]

[Fourier feature mapping]

함수 $\gamma(\cdot)$ 는 $\mathbf{x}$ 의 세 좌표값 각각에 별도로 적용되며([-1, 1] 범위로 정규화), $\mathbf{d}$의 세 구성 요소에도 적용된다(이 값들도 구조적으로 [-1, 1] 범위에 존재).

실험에서는 L = 10 for $\gamma(\mathbf{x})$, L = 4 for $\gamma(\mathbf{d})$ 로 설정했다.

시점 의존성을 제거한 모델은 반사광(specularities)을 표현하는 데 어려움을 겪음을 보여준다. 따라서, 객체의 세밀한 부분을 잘 표현하기 위해 바로 옆 픽셀과의 차이를 고차원으로 표현해 잘 학습할 수 있도록 하자.

Hierarchical volume sampling

N개의 쿼리 지점에서 ray를 등분해 불연속적인 간격의 포인트를 샘플링하는 렌더링 전략은 빈 공간과 가려진 영역이 반복적으로 샘플링되어 continuous하지 못한 모델이 된다.

따라서, 해당 논문에서는 각 구간에서는 일정한 간격(1차), 각 구간 내에서는 랜덤하게 샘플을 할당(2차)하는 계층적 표현을 제안한다.

  • Random Sampling

    • Coarse model

      $[t_n, t_f]$를 N개의 균등한 bin으로 나눠 각 간격에서 무작위로 하나의 샘플을 균일하게 추출하는 층화 샘플링(stratified sampling) 접근 방식을 사용한다.

      \[ t_i \sim U \left( t_n + \frac{i - 1}{N}(t_f - t_n), \, t_n + \frac{i}{N}(t_f - t_n) \right) \]

    • Fine model

      • Inverse transform samling

        : ray내 density가 높은 부분 즉, 영향력이 큰 부분에 대해 추가적 Sampling을 진행해 전체 모델을 완성한다.

        : 1차 샘플링 좌표들에 대해 color 값들을 계산한 후에, 앞서 사용한 불투명도인 wi를 사용해 이러한 weight값(d x T())를 $\hat{w}i = \frac{w_i}{\sum{j=1}^{N_c} w_j}$로 Normalize하면 부분별로 상수로 나타나는 확률 밀도 함수(PDF)가 생성되어 ray 내의 난수값으로 두번째 $N_f$ 위치 집합을 샘플링한다.

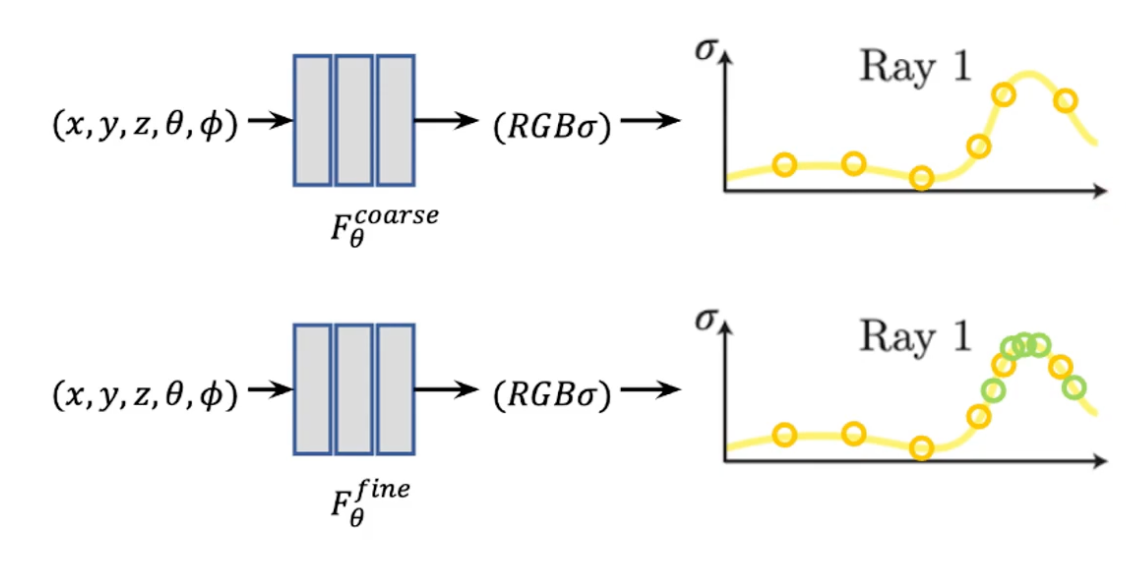      coarse 64, fine 128이라 가정했을 때 coarse network에서 사용했던 weight 값(alpha x T())와 비슷한 분포를 가지는 point 128개 sampling

위 샘플링 방법은 연속적인 장면 표현을 가능하게 해 C(r)을 추정하게 된다. 아래는 코드에 적용하도록 적분을 summation 형태으로 근사한 식이다.

즉, 결과(2D Pixel의 좌표 color)는 3D voxel 좌표 color와 불투명도에 대한 weighted sum이다.

\[\hat{C}(r) = \sum_{i=1}^{N} T_i (1 - \exp(-\sigma_i \delta_i)) c_i, \quad T_i = \exp \left( - \sum_{j=1}^{i-1} \sigma_j \delta_j \right)\]
  • $δ_i = t_{i+1} − t_i$: 인접한 샘플 간의 거리
  • $T_i$; i번째 Voxel이 보일 확률

  • $(1 - \exp(-\sigma_i \delta_i))$: i번쨰 Voxel이 Surface일 확률, MLP를 통한 volume density 값이 클수록 i번째 voxel의 color 영향력이 커진다.

    알파 값 $α_i = 1 − exp(−σ_iδ_i)$ 을 사용하여 $(c_i, σ_i)$ 값 집합에서 $\hat{C}(r)$ 을 계산 가능하게 한다.

  • $\hat{C}(r)$ 식에서 coarse 네트워크의 알파 합성 색을 ray에 따라 샘플링된 모든 색상 $c_i$의 weighted sum으로 재작성한 출력을 기반으로 관련된 volume 부분을 향해 편향된 샘플링 지점을 생성한다.
\[\hat{C}c(r) = \sum{i=1}^{N_c} w_i c_i, \quad w_i = T_i(1 - \exp(-\sigma_i \delta_i)).\]

위 과정은 첫 번째와 두 번째 샘플 집합의 결합에서 “fine” 네트워크를 평가하고 $\hat{C}(r)$ 식을 사용하여 모든 $N_c + N_f$ 샘플을 사용해 광선의 최종 렌더링된 색상 $\hat{C}_f(r)$을 계산한다.

따라서, coarse → fine 과정에서 density가 높은 지점에서 더 많은 샘플링을 수행해 volume rendering을 진행한다.

Implementation details

‘각 scene’에 대해 ‘별도’의 신경 연속 체적 표현 네트워크를 최적화할 때 최적화의 각 반복에서 데이터셋의 모든 픽셀 집합에서 무작위로 카메라 광선 배치를 샘플링하고 계층적 샘플링을 따라

  • “coarse” 네트워크에서 $N_c$ 샘플
  • “fine” 네트워크에서 $N_c + N_f$ 샘플

을 쿼리한다.

그 다음 volume rendering을 사용하여 두 샘플 집합 모두에서 각 광선의 색상을 렌더링한다.

여기서 손실 함수는 “coarse” 및 “fine” 렌더링에 대해 렌더링된 픽셀 색상과 실제 픽셀 색상 간의 총 제곱 오차로 정의된다.

  • Loss Function
\[L = \sum_{r \in R} \left[ \left( \hat{C}_c(r) - C(r) \right)^2 + \left( \hat{C}_f(r) - C(r) \right)^2 \right]\]

R: 각 배치의 광선 집합

$C(r)$: 각각 광선 r에 대한 실제 값(Ground Truth)

$\hat{C}_c(r)$: “coarse” 볼륨 예측 값

$\hat{C}_f(r)$: “fine” 볼륨 예측 값

모든 예측에 대해 GT와의 Loss를 각각 구하여 MSE를 계산해 전체 loss 계산을 한다.

최종 렌더링은 $\hat{C}_f(r)$ 에서 생성되지만, “coarse” 네트워크의 가중치 분포가 “fine” 네트워크에서 샘플을 할당하는 데 사용될 수 있도록  $\hat{C}_c(r)$ 의 손실도 최소화한다.

Results

해당 모델은 quantitatively, qualitatively으로 우수한 결과를 보여주었다.

  • Datasets

    합성 렌더링 데이터셋(’Diffuse Synthetic 360°’, ‘Realistic Synthetic 360°’)

    • DeepVoxels: 512x512 pixel rendering
      • Input: 479 viewpoints
      • Test: 1000 viewpoints
      • 상부반구에서 샘플링
    • 자체 데이터셋: 800x800 pixel rendering
      • Input: 100 viewpoints
      • Test: 200 viewpoints
      • 6개 객체: 상부반구에서 샘플링
      • 2개 객체: 전체구에서 샘플링
    • batch size: 4096 rays
    • $N_c = 64$ 좌표에서 “coarse” Volume Sampling
    • $N_f = 128$ 추가 좌표에서 “fine” Volume Sampling
    • Optimizer: Adam

    단일 장면에 대한 최적화는 일반적으로 NVIDIA V100 GPU 한 대에서 10만30만 번의 반복에 걸쳐 수렴하며, 약 12일이 소요된다.

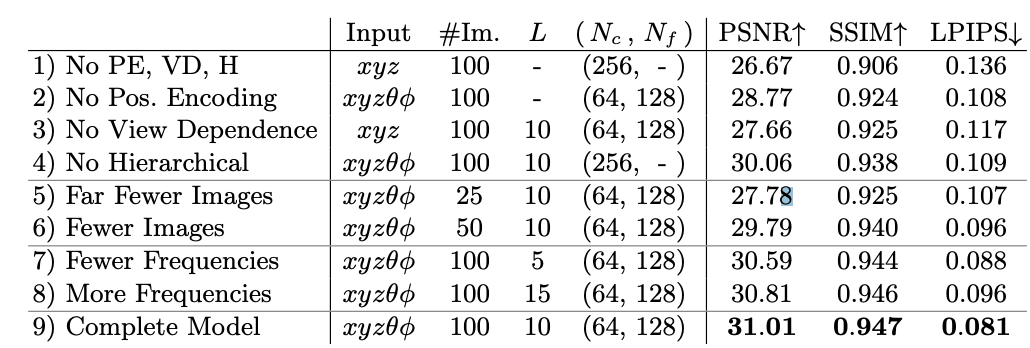
    PSNR/SSIM(값이 클수록 good)과 LPIPS(값이 작을수록 good)을 보고한 method quantitatively(정량적) 우수성 표

    • PSNR: 최대 신호 대 잡음비, 두 이미지간 픽셀 오차가 적을수록 값이 높아짐
    • SSIM: 구조적 유사성 측정값, 값이 높을수록 유사도가 높아짐
    • LPIPS: 이미지 패치 사이의 거리, 계산 값이 작을수록 유사도가 높음

Discussion

  • training할 때, network main(weights)만 가지고 있으면 되기 때문에 memory efficiency하다

  • NeRF는 General한 모델이 아니라 한 Model로 하나의 물체만 만들어낼 수 있는 개념이고, 학습시간도 오래걸려 실생활에 사용하기 상당히 inefficient하다.

    따라서, train/inference 속도를 개선시키거나 dynamic한 물체 렌더링 연구, 입력 이미지를 최소화, Depth 추정을 위한 아래와 같은 후속연구가 꾸준히 진행되었다.

    ⇒ Instant-NeRF, HybridNeRF_렌더링속도개선, MVD^2_입력이미지축소, ViewFusion, Lightplane_메모리축소, Di-NeRF_포즈추정, VR-Nerf

PAPER REVIEW
paper review nerf
This post is licensed under CC BY 4.0 by the author.